RS Aggarwal Class 8 Math Sixth Chapter Operation on Algebric Expressions Exercise 6C Solution
EXERCISE 6C
(1) Divide:
(i) 24x2y3 by 3xy
= 8xy2
(ii) 36xyz2 by – 9xz
= – 4yz
(iii) – 72x2y2z by – 12xyz
= 6xy
(iv) – 56mnp2 by 7mnp
= – 8p
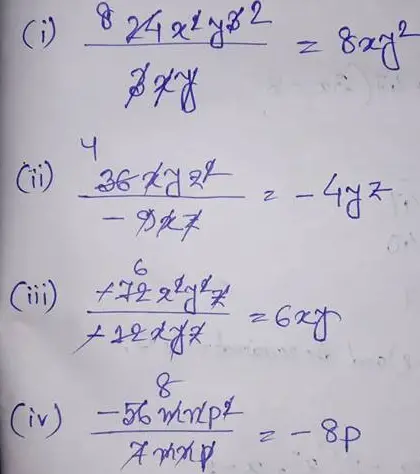
(2) Divide:
(i) 5m3 – 30m2 + 45m by 5m
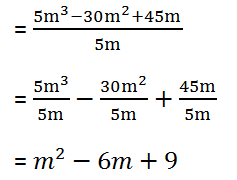
(ii) 8x2y2 – 6xy2 + 10x2y2 by 2xy
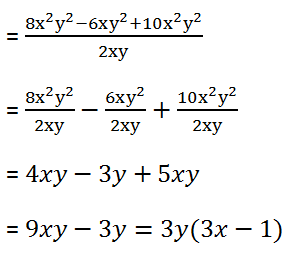
(iii) 9x2y – 6xy + 12xy2 by – 3xy
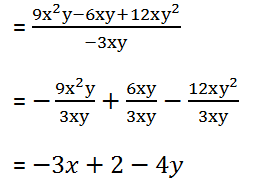
(iv) 12x4 + 8x3 – 6x2 by – 2x2
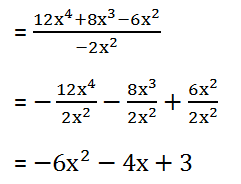
Write the quotient and remainder when we divide:
(3) (x2 – 4x + 4) by (x – 2)
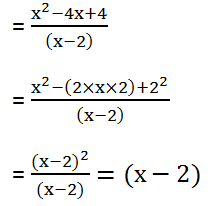
(4) (x2 – 4) by (x + 2)
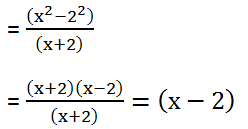
(5) (x2 + 12x + 35) by (x + 7)
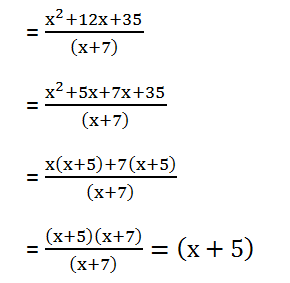
(6) (15x2 + x – 6) by (3x + 2)
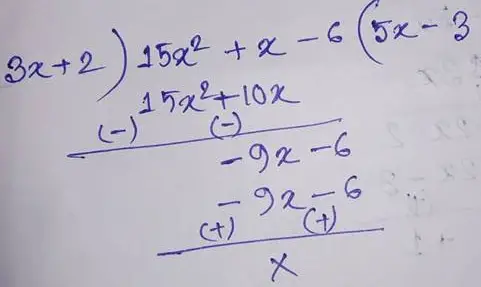
(7) (14x2 – 53x + 45) by (7x – 9)
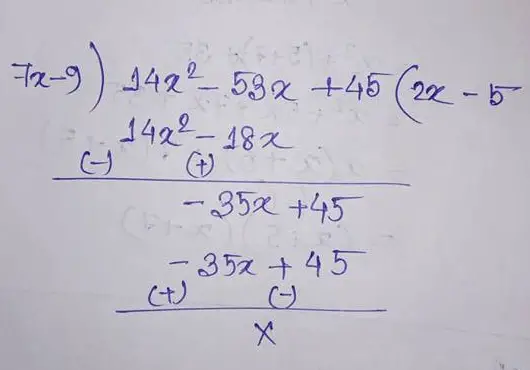
(8) (6x2 – 31x + 47) by (2x – 5)
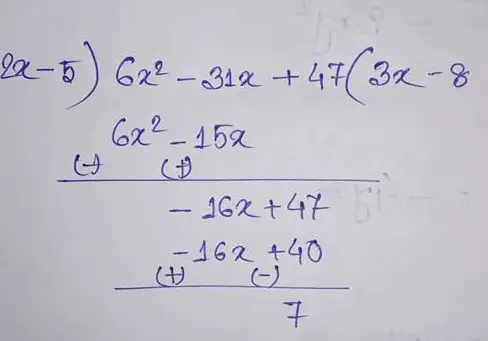
Therefore the quotient is (3x – 8) and the reminder is 7.
(9) (2x3 + x2 – 5x – 2) by (2x + 3)
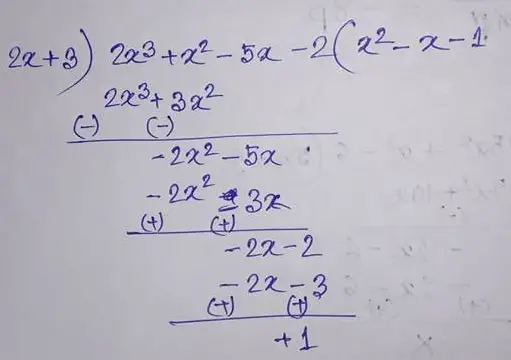
Therefore the quotient is (x2 – x – 1) and the remainder is 1.
(10) (x3 + 1) by (x + 1)
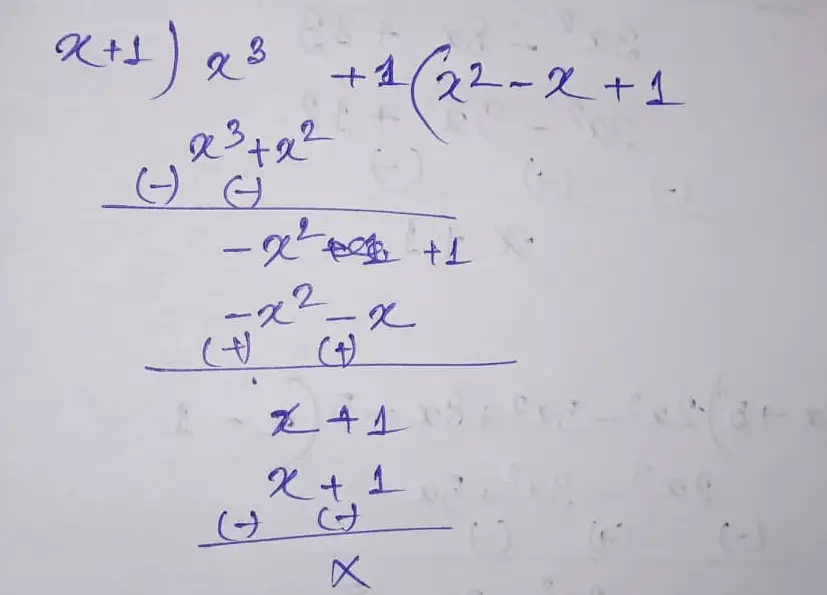
Therefore the quotient is (x2 – x + 1) and the remainder is 0.
(11) (x4 – 2x3 + 2x2 + x + 4) by (x2 + x + 1)
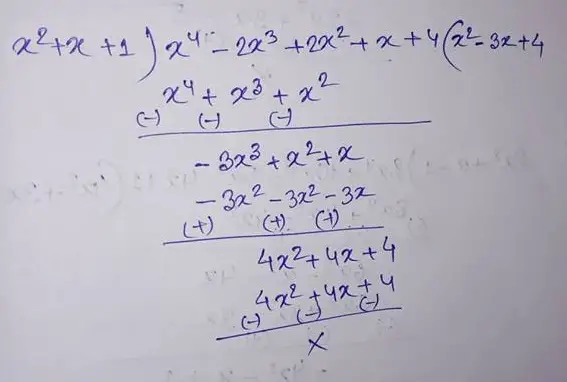
Therefore the quotient is (x2 – 3x + 4) and the remainder is 0.
(12) (x3 – 6x2 + 11x – 6) by (x2 – 5x + 6)
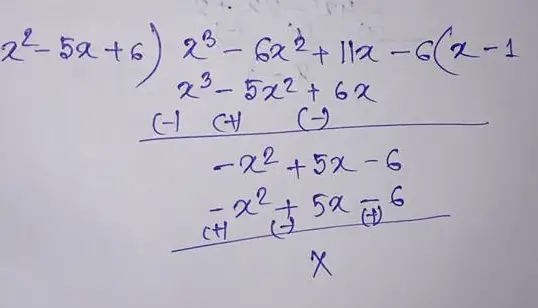
Therefore the quotient is (x – 1) and the remainder is 0.
(13) (5x3 – 12x2 + 12x + 13) by (x2 – 3x + 4)
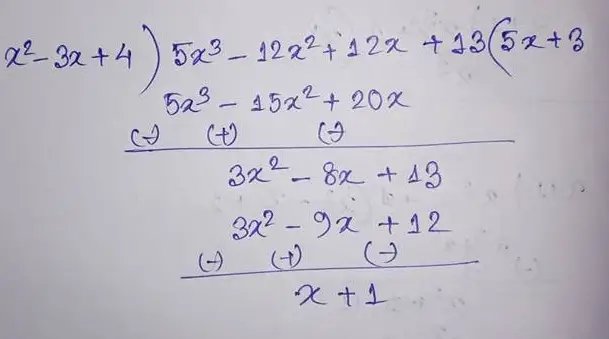
Therefore the quotient is (5x + 3) and the remainder is (x + 1).
(14) (2x3 – 5x2 + 8x – 5) by (2x2 – 3x + 5)
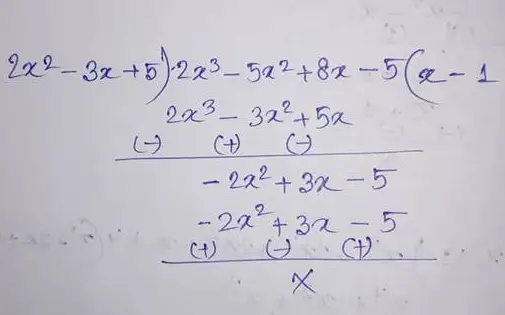
Therefore the quotient is (x – 1) and the remainder is 0.
(15) (8x4 + 10x3 – 5x2 – 4x + 1) by (2x2 + x – 1)
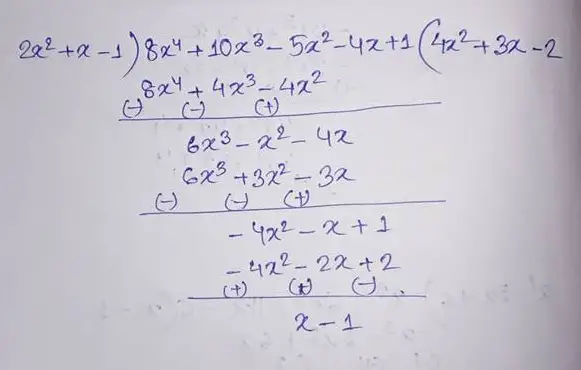
Therefore the quotient is (4x2 + 3x – 2) and the remainder is (x – 1).
Leave a Reply