RS Aggarwal Class 7 Mathematics Twentieth Chapter Mensuration Exercise 20D Solution
EXERCISE 20D
(1) Find the area of the triangle in which
(i) Base = 42 cm and height = 25 cm,
Solution: Area = (1/2 × 42 × 25) cm2 = 525 cm2
(ii) Base = 16.8 m and height = 75 cm.
Solution: Here, 75 cm = 0.75 m
Area = (1/2 × 16.8 × 0.75) m2 = 6.3 m2
(iii) Base = 8 dm and height = 35 cm.
Solution: Here, 8 dm = 80 cm
Area = (1/2 × 80 × 35) cm2 = 1400 cm2.
(2) Find the height of a triangle having an area of 72 cm2 and base 16 cm.
Solution: Let height be x cm.
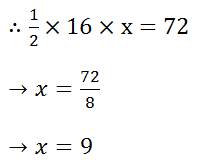
Hence, height of the triangle is 9 cm.
(3) Find the height of a triangular region having an area of 224 m2 and base 28 m.
Solution: Let the height be x m.
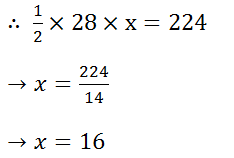
(4) Find the base of a triangle whose area is 90 cm2 and height 12 cm.
Solution: Let the base be x cm.
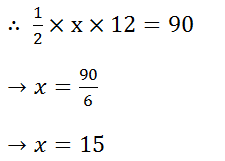
Hence, the base of the triangle is 15 cm.
(5) The base of a triangular field is three times its height. If one of the cultivating the field at Rs 1080 per hectare is Rs 14580, find its base and height.

(6) The area of right triangular region is 129.5 cm2. If one of the sides containing the right angle is 14.8 cm, find the other one.

(7) Find the area of a right triangle whose base is 1.2 m and hypotenuse 3.7 m.

(8) The legs of a right triangle are in the ratio 3 : 4 and its area is 1014 cm2. Find the lengths of its legs.

(9) One side of a right-angled triangular scarf is 80 cm and its longest side is 1 m. Find its cost at the rate of Rs 250 per m2.

(10) Find the area of an equilateral triangle each of whose sides measures 9i) 18 cm, (ii) 20 cm.

(11) Area of an equilateral triangle is (16 × √3) cm2. Find the length of each side of the triangle.

(12) Find the length of the height of an equilateral triangle of side 24 cm.

(13) Find the area of the triangle in which
(i) a = 13 m, b = 14 m, c = 15m.
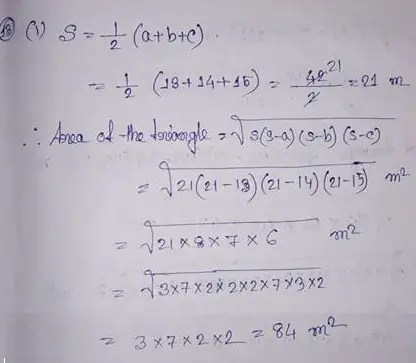
(ii) a = 52 cm, b = 56 cm, c = 60 cm.
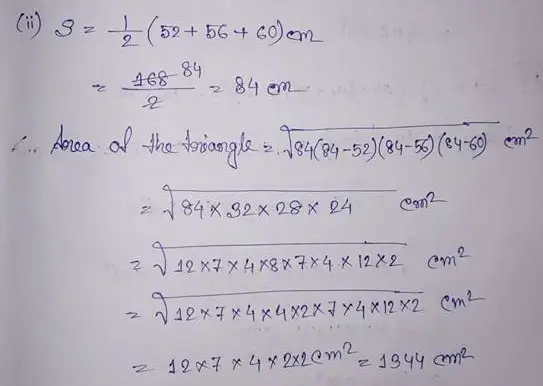
(iii) a = 91 m, b = 98 m, c = 105 m.

(14) The lengths of the sides of a triangle are 33 cm, 44 cm and 55 cm respectively. Find the area of the triangle and hence find the height corresponding to the side measuring 44 cm.
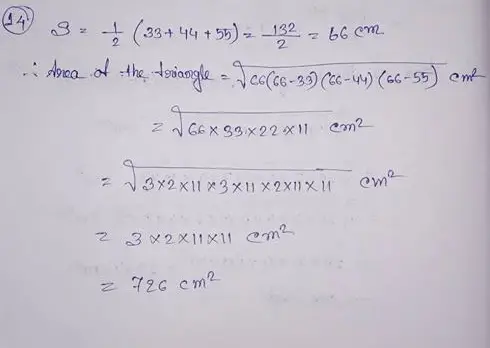
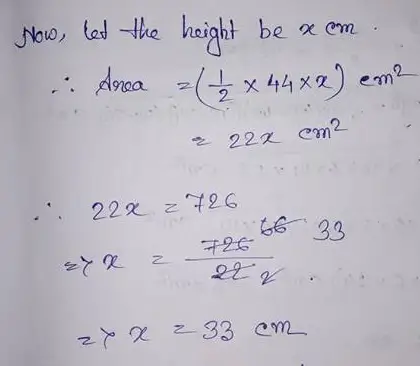
(15) The sides of a triangle are in the ratio 13 : 14 : 15 and its perimeter is 84 cm. Find the area of the triangle.

(16) The sides of a triangle are 42 cm, 34 cm and 20 cm. Calculate its area and the length of the height on the longest side.

(17) The base of an isosceles triangle is 48 cm and one of its equal sides is 30 cm. Find its area of triangle.
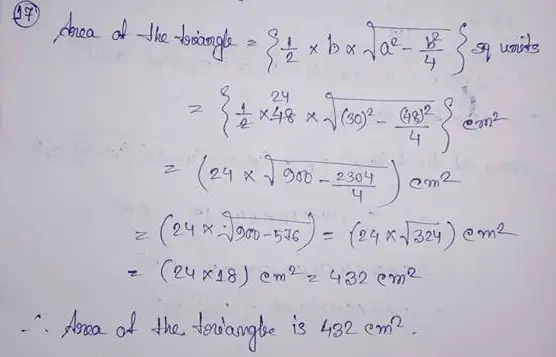
(18) The base of an isosceles triangle is 12 cm and its perimeter is 32 cm. Find its area.
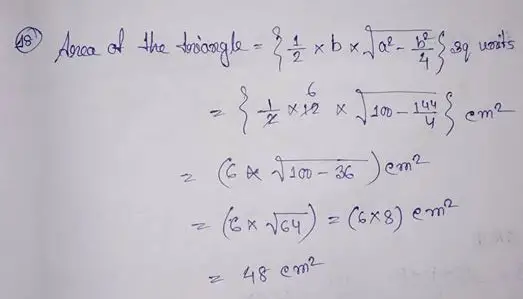
(19) A diagonal of a quadrilateral is 26 cm and perpendiculars drawn to it from the opposite vertices are 12.8 cm and 11.2 cm. Find the area of the quadrilateral.

(20) In a quadrilateral ABCD, AB = 28 cm, BC = 26 cm, CD = 50 cm, DA = 40 cm and diagonal AC = 30 cm. Find the area of the quadrilateral.

(21) In the given figure, ABCD is a rectangle with length = 36 m breadth = 24 m, In ∆ADE, EF ⊥ AD and EF = 15 m. Calculate the area of the shaded region.

(22) In the given figure, ABCD is rectangle in which AB = 40 cm and BC = 25 cm. If P, Q, R,S be the midpoints of AB, BC, CD and Da respectively, find the area of the shaded region.

(23) In the following figures, find the area of the shaded region.


(24) Find the area of quadrilateral ABCD in which diagonal BD = 24 cm. AL ⊥ BD and CM ⊥ BD such that AL = 5 cm and CM = 8 cm.

Leave a Reply