RS Aggarwal Class 7 Mathematics Twentieth Chapter Mensuration Exercise 20C Solution
EXERCISE 20C
(1) Find the area of a parallelogram with base 32 cm and height 16.5 cm.
Solution: Are of the parallelogram = (32 × 16.5) cm2 = 528 cm2.
(2) The base of a parallelogram measures 1 m 60 cm and its height is 75 cm. Find its area in m2.
Solution: Here 1 m 60 cm = 1.60 m and 75 cm = 0.75 m
∴ Area of the parallelogram = (1.60 × 0.75) m2 = 1.2 m2
(3) In a parallelogram it is being given that base = 14 dm and height = 6.5 dm. Find its area in (i) cm2, (ii) m2.
Solution: Here 14 dm = 1.4 m = 140 cm and 6.5 dm = 65/100 = 0.65 m = 65 cm
(i) Now area of parallelogram = (140 × 65) cm2 = 9100 cm2
(ii) Area of parallelogram = (1.4 × 0.65) m2 = 0.91 m2.
(4) Find the height of a parallelogram whose area is 54 cm2 and the base is 15 cm.
Solution: Base of the parallelogram = 54/15 cm = 3.6 cm
(5) One side of a parallelogram is 18 cm long and its area is 153 cm2. Find the distance of the given side from its opposite side.
Solution: Base = 18 cm, Area = 153 cm2
Let the height be x cm.
∴ 18 × x = 153
or, x = 153/18
or, x = 8.5
Hence, the required distance is 8.5 cm.
(6) In a parallelogram ABCD, AB = 18 cm, BC = 12 cm, AL ⊥ DC and AM ⊥ BC.
IF AL = 6.4 cm, find the length of AM.

(7) The adjacent sides of a parallelogram are 15 cm and 8 cm. If the distance between the longer sides is 4 cm, find the distance between the shorter sides.

(8) The height of a parallelogram is one-third of its base. If the area of the parallelogram is 108 cm2, find its base and height.
Solution: Let the base be x cm and its base (1/3)x cm.
Given, area = 108 cm2
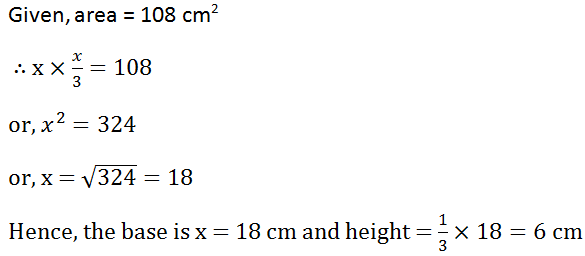
(9) The base of a parallelogram is twice its height. If the area of the parallelogram is 512 cm2, find the base and the height.
Solution: let the height be x cm and base be 2x cm.

Hence, the height is x = 16 cm and base is 2x = 2 × 16 = 32 cm.
(10) Find the area of a rhombus in which
(i) Each side = 12 cm and height = 7.5 cm
Solution: Area of the rhombus = (12 × 7.5) cm2 = 90 cm2.
(ii) Each side = 2 dm and height = 12.6 cm.
Solution: Here, 2 dm = 20 cm
Area of the rhombus = (20 × 12.6) = 252 cm2.
(11) Find the area of a rhombus, the lengths of whose diagonals are:
(i) 16 cm and 28 cm,
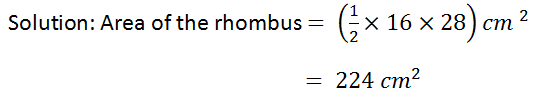
(ii) 8 dm 5 cm and 5 dm 6 cm.
Solution: 8 dm 5 cm = 85 cm and 5 dm 6 cm = 56 cm.

(12) Find the area of a rhombus each side of which measure 20 cm and one of whose diagonals is 24 cm.

(13) The area of a rhombus is 148.8 cm2. If one of its diagonals is 19.2 cm, find the length of the other diagonal.
Solution: Let the length of other diagonal of the rhombus be x cm.
Given, area of rhombus = 148.8 cm2
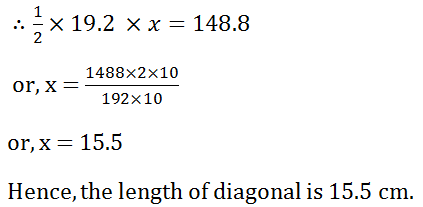
(14) The area of a rhombus is 119 cm2 and its perimeter is 56 cm. Find its height.
Solution: Given, the perimeter = 56 cm
Area = 119 cm2
Side of the rhombus = (56/4) cm = 14 cm
Height of the rhombus = (119/14) cm = 8.5 cm.
(15) The area of a rhombus is 441 cm2 and its height is 17.5 cm. Find the length of each side of the rhombus.
Solution: Base = (441/17.5) cm = 25.2 cm
(16) The area of a rhombus is equal to the area of a triangle having base 24.8 cm and the corresponding height 16.5 cm. If one of the diagonals of the rhombus is 22 cm, find the length of the other diagonal.
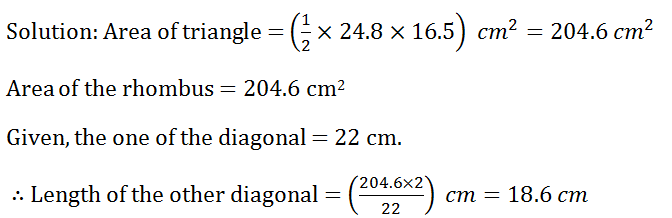
Leave a Reply