RS Aggarwal Class 7 Math Seventh Chapter Linear Equation In One Variable Exercise 7B Solution
EXERCISE 7B
(1) Twice a number when decreased be 7 gives 45. Find the number.
Solution: Let the required number is x.
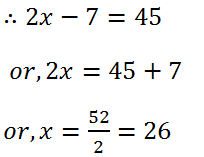
(2) Thrice a number when increased by 5 gives 44. Find the number.
Solution: Let the required number is x.
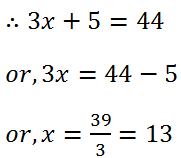
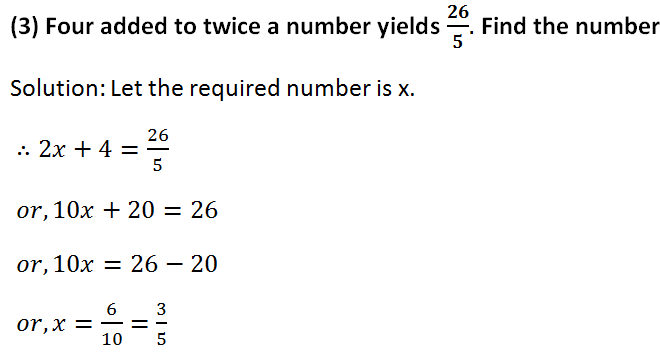
(4) A number when added to its half gives 72. Find the number.
Solution: Let the number is x.
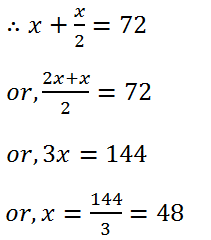
(5) A number added to its two-thirds is equal to 55. Find the number.
Solution: Let the number is x.
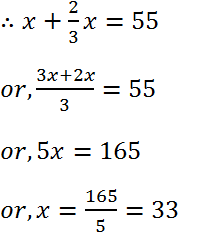
(6) A number when multiplied by 4, exceeds itself by 45. Find the number.
Solution: Let the number is x.
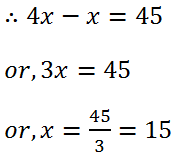
(7) A number is as much greater than 21 as it is less than 71. Find the number.
Solution: Let the number is x.
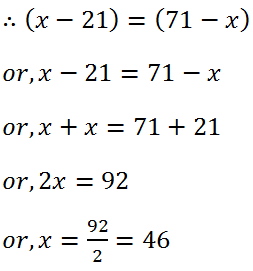
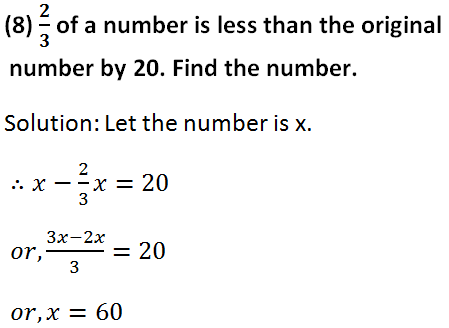
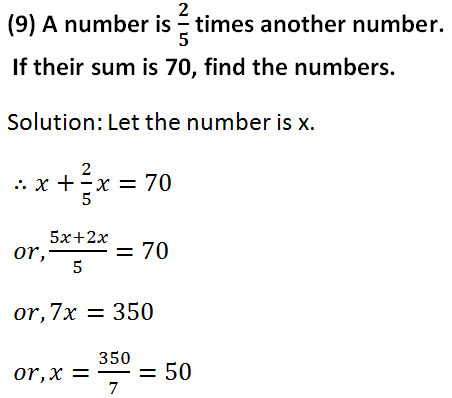
(10) Two-thirds of a number is greater than one-third of the number by 3. Find the number.
Solution: Let the number is x.
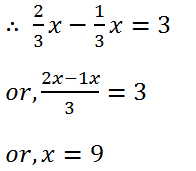
(11) The fifth part of a number when increased by 5 equals its fourth part decreased by 5. Find the number.
Solution: Let the number is x.
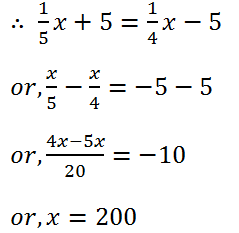
(12) Find two consecutive natural numbers whose sum is 63.
Solution: Let the one number is x and the other is x+1.
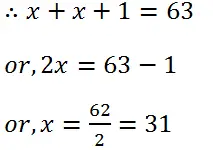
Hence, the one number is 31 and other is (31 + 1) = 32
(13) Find two consecutive positive odd integers whose sum is 76.
Solution: Let the one number is x and other is (x+2).
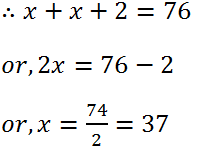
Hence, the one number is 37 and other is 39.
(14) Find three consecutive positive even integers whose sum is 90.
Solution: Let the numbers will be x, (x+2) and (x+4).
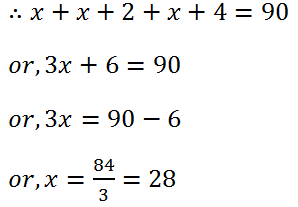
Hence the numbers are 28, (28+2)=30 and (28+4) = 32.
(15) Divide 184 into two parts such that one-third of one part may exceed one-seventh of the other part by 8.
Solution: Let the numbers are x and (184-x).
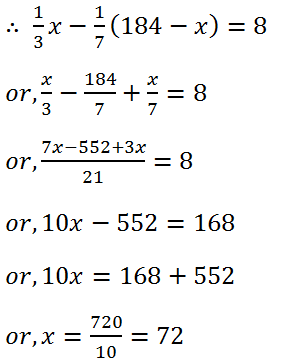
Therefore the numbers are 72 and (184 – 72) = 112.
(16) A sum of Rs 500 is in form of denominations of Rs 5 and Rs 10. If the total number of notes is 90, find the number of notes of each type.
Solution: Let the number of Rs 5 is x and Rs 10 is (90 – x).
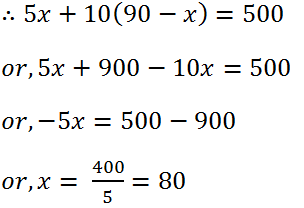
Therefore the number of Rs 5 is 80 and Rs 10 is (90 – 80) = 10.
(17) Sumitra has Rs 34 in 50 paise and 25 paise coins. If the number of 25-paise coins is twice the number of 50-paise coins, how many coins of each kind does she have?
Solution: Let the number of 50-paise coin is x.
And 25-paise coin is 2x.
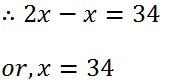
Hence, the number of 50-paise coin is 34 and 25-paise coin is (34×2)=68.
(18) Raju is 19 years younger than his cousin. After 5 years, their ages will be in the ratio 2:3. Find their present ages.
Solution: Let the age of Raju is x years and his cousin is (x+19) years.
After 5 years the age of raju is (x+5) years and his cousin is (x+19+5) years.
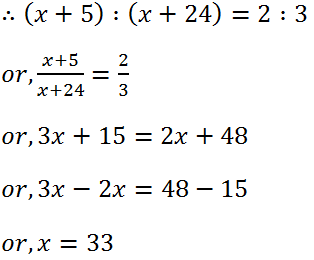
Therefore, the present age of Raju is 33 years and his cousin is (33+19)=52 years.
(19) A father is 30 years older than his son. In 12 years, the man will be three times as old as his son. Find their present ages.
Solution: Let the age of son is x years and his father is (x+30) years.
After 12 years the age of son is (x+12) years and his father is (x+30+12) years.
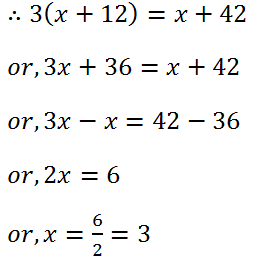
Hence, the age of the son is 3 years and his father is (3+30)=33 years.
(20) The ages of Sonal and Manoj are in the ratio 7:5. Ten years hence, the ratio of their ages will be 9:7. Find their present ages.
Solution: Let, Sonal is 7x years old and Manoj is 5x years old.
After 10 years their age will be (7x+10) and (5x+10) years.
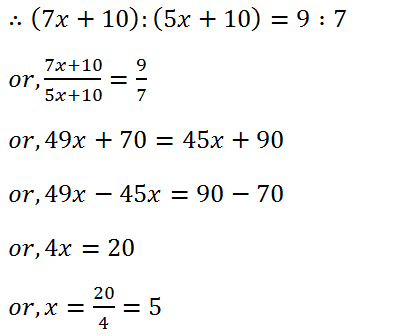
Therefore, Sonal’s present is (7 ×5)=35 years.
And Manoj’s present is (5 ×5)=25 years.
(21) Five years ago a man was seven times as old as his son. Five years hence, the father will be three times as old as his son. Find their present ages.
Solution: Let the present age of son is x years.
5 years ago the age of son is (x – 5) years and father’s age is 7(x – 5) years.
5 years after the age of son is (x + 5) years and father’s age is 3(x+5) years.
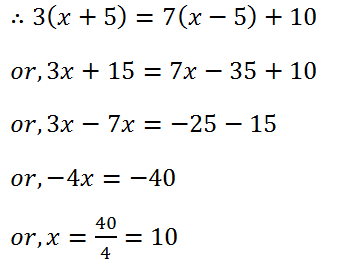
Therefore the present age of son is 10 years and father’s age is 40 years.
(22) After 12 years Manoj will be 3 times as old as he was 4 years ago. Find his present ages.
Solution: Let the present age of Manoj is x years.
4 years ago his age is (x – 4) years.
12 years ago his age is 3(x – 4) years.
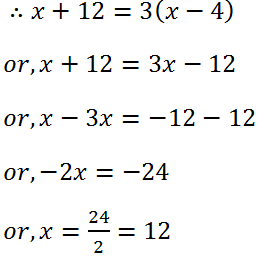
Therefore, the present age of Manoj is 12 years.
(23) In an examination, a student requires 40% of the total marks to pass. If Rupa gets 185 marks and fails by 15 marks, find the total marks.
Solution: Let the total marks is x.
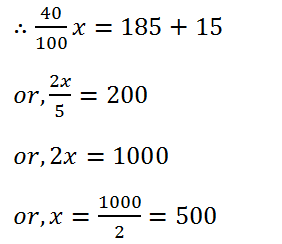
Hence, the total mark is 500.
(24) A number consist of two digits whose sum is 8. If 18 is added to the number its digits are reversed. Find the number.
Solution: Let the one number of the digits is x and other is (8 – x).
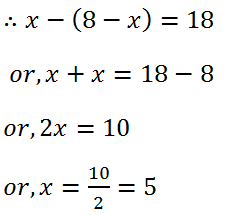
Therefore, the numbers are 5 and (8 – 5) = 3
Hence, the required number is 35.
(25) The total cost of 3 tables and 2 chairs is Rs 1850. If a table costs Rs 75 more than a chair, find the price of each.
Solution: Let the cost of chair is Rs x and cost of a table is Rs (x + 75).
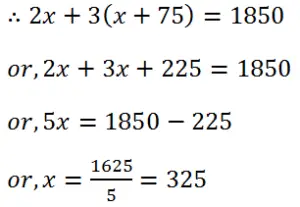
Therefore, the price of a chair is Rs 325 and price of a table is (325 + 75) = Rs 400.
(26) A man sold an article for Rs 495 and gained 10% on it. Find the cost price of the article.
Solution: Let the cost of article is Rs x.
Profit = 10%
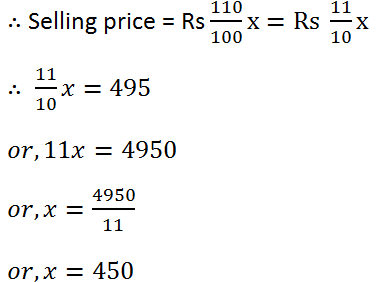
(27) The length of a rectangular field is twice its breadth. If the perimeter of the field is 150 metres, find its length and breadth.
Solution: Let the breadth of the field is x m and length is 2x m.
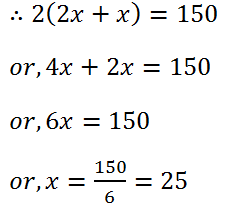
Therefore, the breadth of the field is 25 m and length is (2×25) = 50 m.
(28) Two equal sides of a triangle are each 5 metres less than twice the third side. If the perimeter of the triangle is 55 metres, find the lengths of its sides.
Solution: Let the third side is x.
2nd and 1st side = (2x – 5)+(2x – 5)
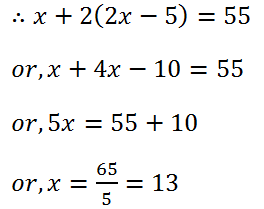
Therefore, the third side is 13 m and 1st and 2nd side is (2×13)-5=21 m.
(29) Two complementary angles differ by 8o. Find the angles.
Solution: Let the angles are x and x.
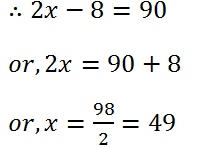
Therefore, the one angle is 49o and other is (90o – 49o) = 41o.
(30) Two supplementary angles differ by 44o. Find the angles.
Solution: Let the angles are x, x.
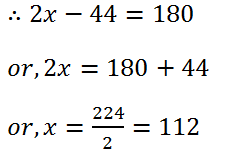
Therefore, the one angles is 112o and other is (180o – 112o) = 68o.
(31) In an isosceles triangle the base angles are equal and the vertex angle is twice of each base angle. Find the measures of the angles of the triangle.
Solution: Let the base angle is x and vertex angle is 2x.
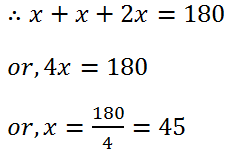
Hence, the base angle is 45o and vertex angle is (2×45o)=90o.

Therefore, the length of his total journey is 80 km.
(33) A labourer is engaged for 20 days on the condition that he will receive Rs 120 for each day he works and will be fined Rs 10 for each day he is absent. If he receives Rs 1880 in all, for how many days did he remain absent?
Solution: Let the number of days of works x days and number of absent days is (20 – x) days.
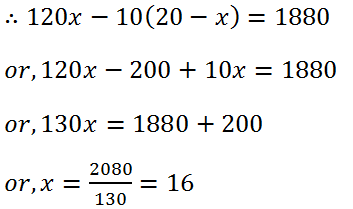
Therefore, the man works 16 days and his absent days is (20 – 16)= 4 days.
(34) Hari Babu left one-third of his property to his son, one-fourth to his daughter and the remainder to his wife. If his wife’s share is Rs 18000, what was the worth of his total property?
Solution: Let the total property of Haribabu is Rs x.
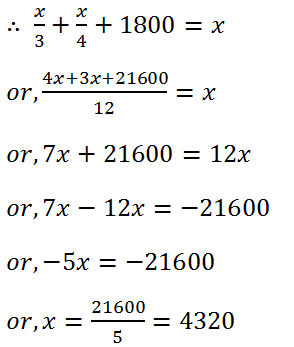
Therefore, Haribabu’s total property is Rs 4320.
(35) How much pure alcohol must be added to 400 mL of a 15% solution to make its strength 32%?
Solution: Let the total amount of alcohol is x mL.
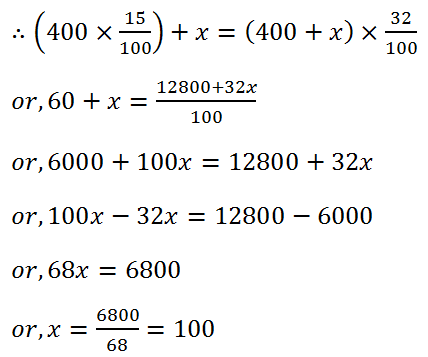
Leave a Reply