RS Aggarwal Class 7 Math Eighth Chapter Ratio and Proportion Exercise 8B Solution

RS Aggarwal Class 7 Math Eighth Chapter Ratio and Proportion Exercise 8B Solution

EXERCISE 8B

(1) Show that 30, 40, 45, 60 are in proportion.

Solution: We have,

Product of extremes = (30 × 60) = 1800

Product of means = (40 × 45) = 1800.

∴ Product of extremes = Product of means.

Hence, 30, 40, 45, 60 are in proportion.

(2) Show that 36, 49, 6, 7 are not in proportion.

Solution: We have,

Product of extremes = (36 × 7) = 252

Product of means = (49 × 6) = 294.

∴ Product of extremes ≠ Product of means.

Hence, 36, 49, 6, 7 are not in proportion.

(3) If 2 : 9 :  : x : 27, find the value of x.

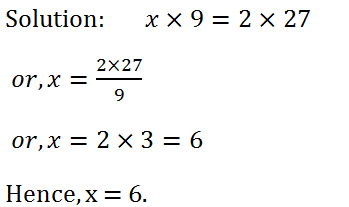
(4) If 8 : x : : 16 : 35, find the value of x.

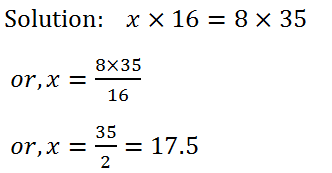
(5) If x : 35 : : 48 : 60, find the value of x.

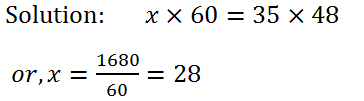
(6) Find the fourth proportional to the numbers:

(i) 8, 36, 6

Solution: Let the fourth term be, x. Then,

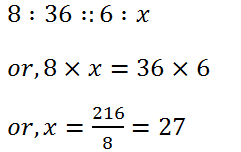
Hence, the fourth term is 27.

(ii) 5, 7, 30

Solution: Let the fourth term be, x. Then,

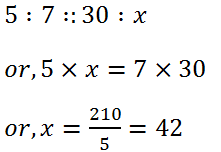
Hence, the fourth term is 42.

(iii) 2.8, 14, 3.5

Solution: Let the fourth term be, x. Then,

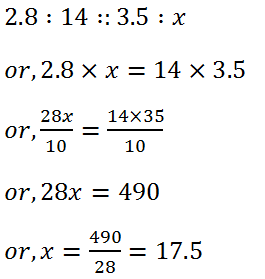
Hence, the fourth term is 17.5.

(7) If 36, 54, x are in continued proportion, find the value of x.

Solution: We have,

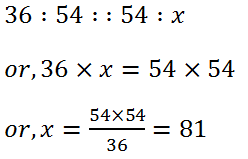
Hence, x = 81.

(8) If 27, 36, x are in continued proportion, find the value of x.

Solution: We have,

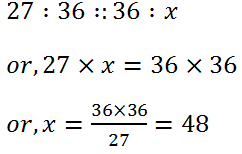
Hence, x = 48.

(9) Find the third proportional to:

(i) 8 and 12

Solution: Let the third proportional be x.

Then, the fourth proportional to 8, 12, 12 is x.

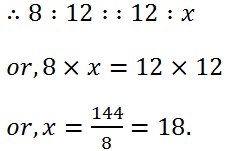
Hence, the third proportional to 9 and 12 is 18.

(ii) 12 and 18

Solution: Let, the third proportional be x.

Then, the fourth proportional to 12 and 18, 18 is x.

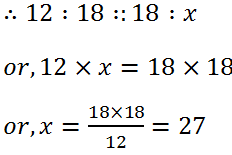
Hence, the third proportional is 27.

(iii) 4.5 and 6

Solution: Let the third proportional be x.

Then, the fourth proportional to 4.5 and 6, 6 is x.

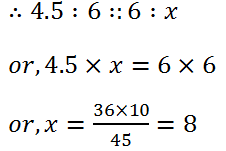
Hence, the third proportional is 8.

(10) If the third proportional to 7 and x is 28. Find the value of x.

Solution: We have,

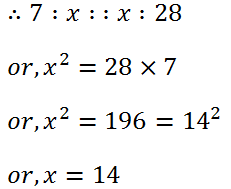
(11) Find the mean proportional between:

(i) 6 and 24

Solution: Let the mean proportional between 6 and 24 be x.

Then, 6 : x : : x : 24

or, x × x = 6 × 24

or, x² = 144 = (12)²

or, x = 12

(ii) 3 and 27

Solution: Let the mean proportional between 3 and 27 be x.

Then, 3 : x : : x : 27

or, x × x = 3 × 27

or, x² = 81 = (9)²

or, x = 9

(iii) 0.4 and 0.9

Solution: Let the mean proportional between 0.4 and 0.9 be x.

Then, 0.4 : x : : x : 0.9

or, x × x = 0.4 × 0.9

or, x² = 0.36 = (0.6)²

or, x = 0.6

(12) What number must be added to each of the numbers 5, 9, 7, 12 to get the numbers which are in proportion?

Solution: Let the number to be added be x. Then,

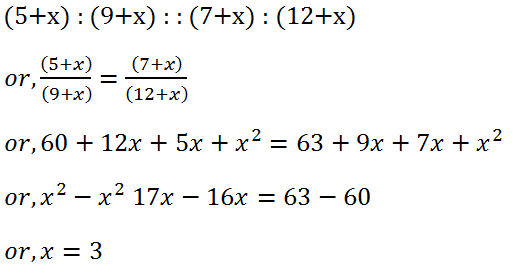
Hence, the required number is 3.

(13) What number must be subtracted from each of the numbers 10, 12, 19, 24 to get the numbers which are in proportion?

Solution: Let the number to be subtracted be x. then,

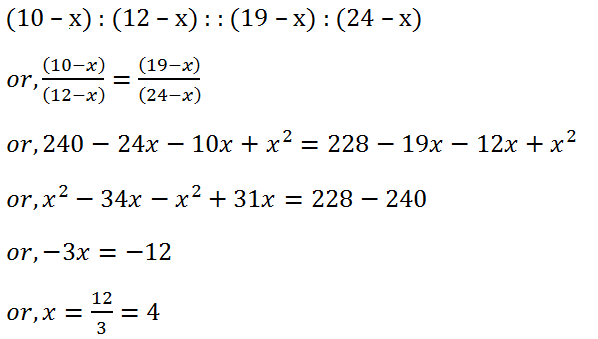
Hence, the required number is 4.

(14) The scale of map is 1 : 5000000. What is the actual distance between two towns, if they are 4 cm apart on the map?

Solution: 1 cm on the map shows the distance = 5000000 cm.

4 cm on the map shows the distance = (50 × 4) km = 200 km.

∴ Actual distance between the two towns is 200 km.

(15) At a certain time a tree 6 m high casts a shadow of length 8 metres. At the same time a pole casts a shadow of length 20 metres. Find the height of the pole.

Solution: Let the height of pole is x m.

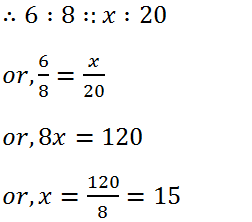
Hence, the height of the pole is 15 m.