RS Aggarwal Class 7 Math Eighth Chapter Ratio and Proportion Exercise 8A Solution

RS Aggarwal Class 7 Math Eighth Chapter Ratio and Proportion Exercise 8A Solution

EXERCISE 8A

(1) Express each of the following rations in simplest form:

(i) 24 : 40

= (24 ÷ 8) : (40 ÷ 8)

= 3 : 5

(ii) 13.5 : 15

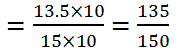
= 135 : 150

= (135 ÷ 15) : (150 ÷ 15)

= 9 : 10

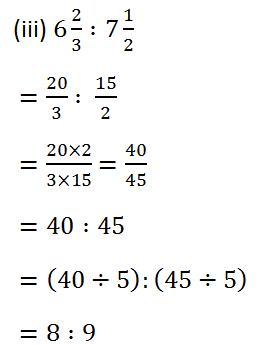
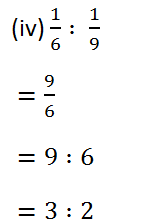
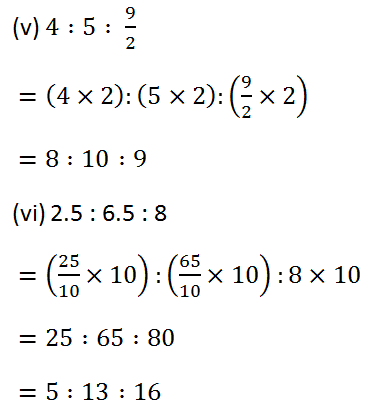
(2) Express each of the following rations in simplest form:

(i) 75 paise : 3 rupees

Here 3 rupees = 300 paise

= 75 : 300

= (75 ÷ 75) : (300 ÷ 75)

= 1 : 4

(ii) 1 m 5 cm : 63 cm

Here 1 m 5 cm = 105 cm

= 105 cm : 63 cm

= (105 ÷ 21) cm : (63 ÷ 21) cm

= 5 cm : 3 cm

(iii) 1 hour 5 minutes : 45 minutes

Here 1 hour 5 minutes = 65 minutes

= 65 : 45

= (65 ÷ 5) : (45 ÷ 5)

= 13 : 9

(iv) 8 months : 1 year

Here, 1 year = 12 months

= 8 : 12

= (8 ÷ 4) : (12 : 4)

= 2 : 3

(v) (2 kg 250 g) : 3 kg

Here, 2 kg 250 g = 2250 g

3 kg = 3000 g

= 2250 : 3000

= (2250 ÷ 750) : (3000 ÷ 750)

= 3 : 4

(vi) 1 km : 750 m

Here, 1 km = 1000 m

= 1000 : 750

= 100 : 75

= (100 ÷ 25) : (75 ÷ 25)

= 4 : 3

(3) If A : B = 7 : 5 and B : C = 9 : 14, find A : C.

Solution: A : B = 7 : 5 and B : C = 9 : 14

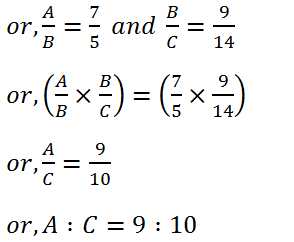
(4) If A : B = 5 : 8 and B : C = 16 : 25, find A : C.

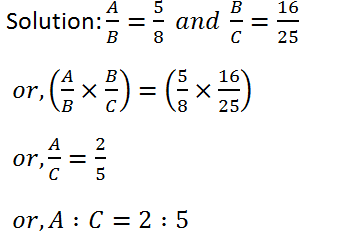
(5) If A : B = 3 : 5 and B : C = 10 : 13, find A : B : C.

Solution: A : B = (3 × 2) : (5 × 2) = 6 : 10

∴ A : B : C = 6 : 10 : 13

(6) If A : B = 5 : 6 and B : C = 4 : 7, find A : B : C.

Solution: A : B = (5 × 2) : (6 × 2) = 10 : 12

B : C = (4 × 3) : (7 × 3) = 12 : 21

∴ A : B : C = 10 : 12 : 21

(7) Divide Rs 360 between Kunal and Mohit in the ratio 7 : 8.

Solution: Sum of the ratio terms = (7 + 8) = 15

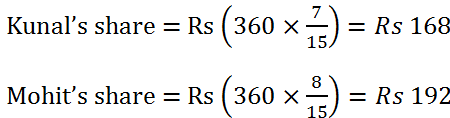
(9) Divide Rs 5600 between A, B and C in the ratio 1 : 3 : 4.

Solution: Sum of the ratio terms =(1+3+4)=8

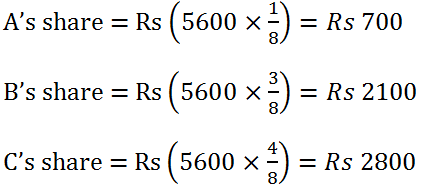
(10) What number must be added to each term of ratio 9 : 16 to make the ratio 2 : 3?

Solution: Let the required number to be added be x. Then, we have,

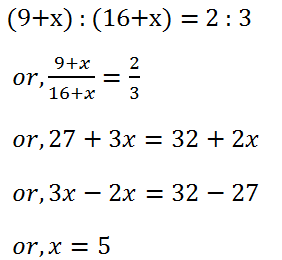
Hence, the required number is 5.

(11) What number must be subtracted from each term of the ratio 17 : 33 so that the ratio becomes 7 : 15?

Solution: Let the required number is x. Then, we have,

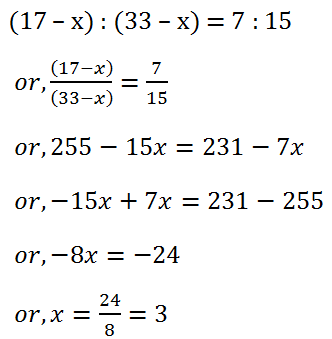
Hence, the required number is 3.

(12) Two numbers are in the ratio 7 : 11. If 7 is added to each term of the ratio becomes 2 : 3. Find the numbers.

Solution: Let the required number is x. Then, we have,

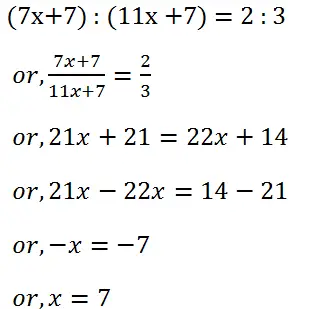
Hence the numbers are (7×7) = 49 and (11×7) = 77.

(13) Two numbers are in the ratio 5 : 9. On subtracting 3 from each, the ratio becomes 1 : 2. Find the numbers.

Solution: Let the required number is x. Then, we have,

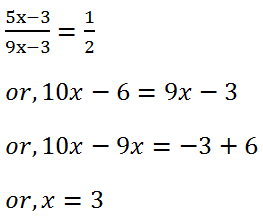
Hence, the required numbers are (5×3) = 15 and (9×3) = 27.

(14) Two numbers are in the ratio 3 : 4. If their LCM is 180, find the numbers.

Solution: Let the required numbers be 3x and 4x.

Then, their LCM is 12x.

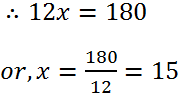
Hence, the numbers are (3×15)=45 and (4×15) = 60.

(15) The ages of A and B are in the ratio 8 : 3. Six years hence, their ages will be in the ratio 9 : 4. Find their present ages.

Solution: Let the present ages of A and B be 8x and 3x years respectively.

A’s age after 6 years = (8x + 6) years.

B’s age after 6 years = (3x+6) years.

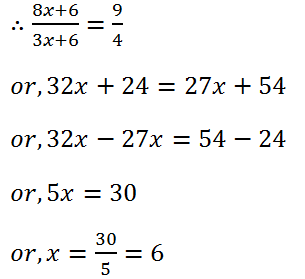
Therefore, A’s present age = (8×6) = 48 years.

B’s present age = (3×6)=18 years.

(16) The ratio of copper and zinc in an alloy is 9 : 5, If the weight of copper in the alloy is 48.6 grams, find the weight of zinc in the alloy.

Solution: Let the weight of copper is 9x grams and zinc is 5x grams.

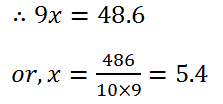
Therefore, the weight of the zinc is (5×5.4)=27 grams.

(17) The ratio of boys and girls in a school is 8 : 3. If the total number of girls be 375, find the number of boys in the school.

Solution: Let the number of boys and girls will be 8x and 3x.

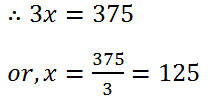
Therefore, the numbers are boy is (8×125)=1000.

(18) The ratio of monthly income to the savings of a family is 11 : 2. If the savings be Rs 2500, find the income and expenditure.

Solution: Let the income and savings will be 11x and 2x.

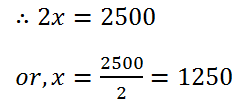
Therefore, the income is (11×1250) = Rs 13750.

And expenditure is Rs (13750 – 2500) = Rs 11250.

(19) A bag contains Rs 750 in the form of rupee, 50 P and 25 P coins n the ratio 5 : 8 : 4. Find the number of coins of each type.

Solution: Let the number of rupee , 50 p and 25 p coins be 5x, 8x and 4x.

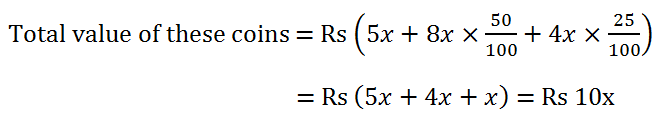
But the total coins = Rs 750.

∴10x = 750

or, x=75

Number of 1 rupee coins = 5 × 75 = 375

Number of 50 p coins = 8 × 75 = 600

Number of 25 p coins = 4 × 75 = 300

(20) If (4x+5) : (3x+11) = 13 : 17, find the value of x.

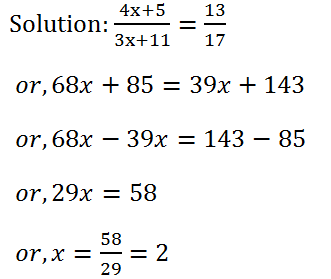
(21) If x : y = 3 : 4, find (3x + 4y) : (5x + 6y).

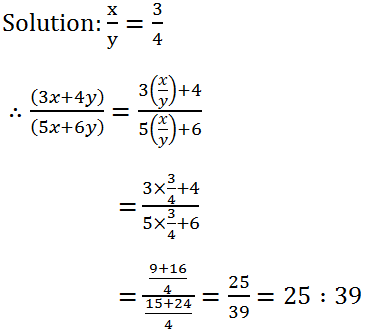
(22) If x : y = 6 : 11, find (8x – 3y) : (3x + 2y).

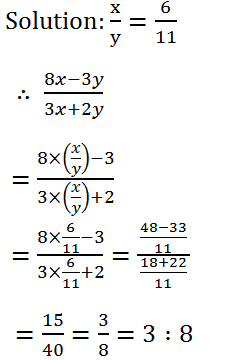
(23) Two numbers are in the ratio 5 : 7. If the sum of the numbers is 720, find the numbers.

Solution: Let the numbers will be 5x and 7x.

Hence, the numbers are (5 ×60) = 300 and (7 ×60) = 420.

(24) Which ratio is greater?

(i) (5 : 6) or (7 : 9)

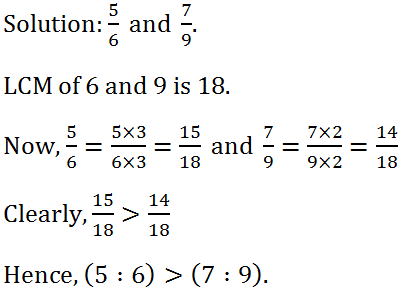
(ii) (2 : 3) or (4 : 7)

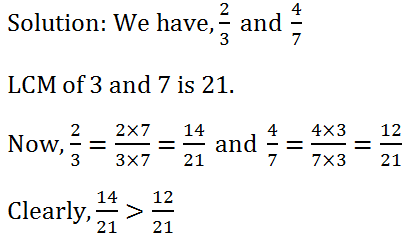
Hence, (2 : 3) >(4 : 7)

(iii) (1 : 2) or (4 : 7)

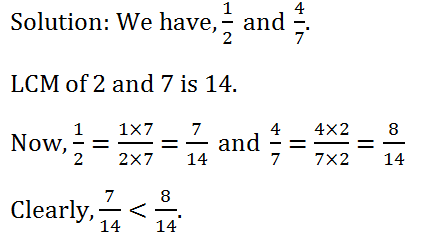
Hence, (1 :2)<(4 :7).

(iv) (3 : 5) or (8 : 13)

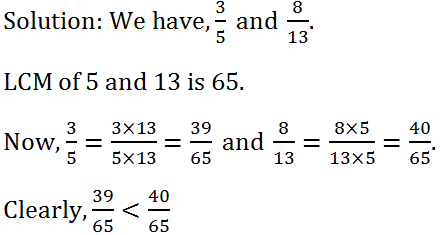
(25) Arrange the following ratios in ascending order:

(i) (5 : 6), (8 : 9), (11 : 18)

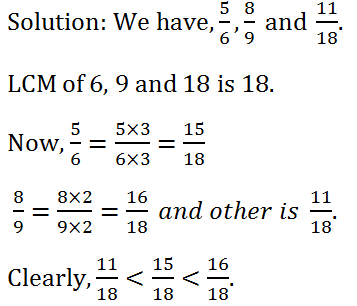
Hence, (11 : 18)< (5 : 6)< (8 : 9).

(ii) (11 : 14), (17 : 21), (5 : 7) and (2 : 3)

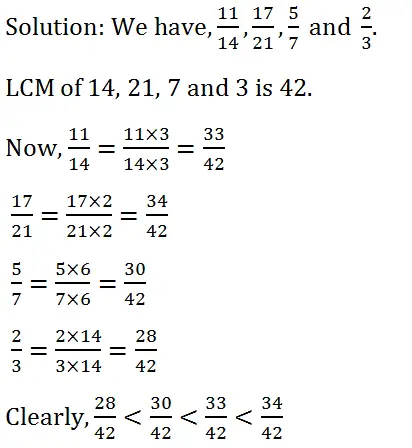
Hence, (2 :3)<(5 :7)<(11 :14)<(17 :21).