NCERT Class 6 Mathematics Third Chapter Playing with Numbers Exercise 3.6 Solutions

NCERT Class 6 Mathematics Third Chapter Playing with Numbers Exercise 3.6 Solutions

EXERCISE 3.6

(1) Find the HCF of the following numbers:

(a) 18, 48

Solution: The HCF of 18 and 48 can also be found by prime factorization of these numbers as follows:

Thus, 18 = 2 × 3 × 3

48 = 2 × 2 × 2 × 2 × 3

∴ HCF of 18 and 48 is 2 × 3 = 6.

(b) 30, 42

Solution: The HCF of 30 and 42 can also be found by prime factorization of these numbers as follows:

Thus, 30 = 2 × 3 × 5

42 = 2 × 3 × 7

∴ HCF of 30 and 42 is 2 × 3 = 6.

(c) 18, 60

Solution: The HCF of 18 and 60 can also be found by prime factorization of these numbers as follows:

Thus, 18 = 2 × 3 × 3

60 = 2 × 2 × 3 × 5

∴ HCF of 18 and 60 is 2 × 3 = 6.

(d) 27, 63

Solution: The HCF of 27 and 63 can also be found by prime factorization of these numbers as follows:

Thus, 27 = 3 × 3 × 3

63 = 3 × 3 × 7

∴ HCF of 27 and 63 is 3 × 3 = 9.

(e) 36, 84

Solution: The HCF of 36 and 84 can also be found by prime factorization of these numbers as follows:

Thus, 36 = 2 × 2 × 3 × 3

84 = 2 × 2 × 3 × 7

∴ HCF of 36 and 84 is 2 × 2 × 3 = 12.

(f) 34, 102

Solution: The HCF of 34 and 102 can also be found by prime factorization of these numbers as follows:

Thus, 34 = 2 × 17

102 = 2 × 3 × 17

∴ HCF of 34 and 102 is 2 × 17 = 34.

(g) 70, 105, 175

Solution: The HCF of 70, 105 and 175 can also be found by prime factorization of these numbers as follows:

Thus, 70 = 2 × 5 × 7

105 = 3 × 5 × 7

175 = 5 × 5 × 7

∴ HCF of 70, 102 and 175 is 5 × 7 = 35.

(h) 91, 112, 49

Solution: The HCF of 91, 112 and 49 can also be found by prime factorization of these numbers as follows:

Thus, 91 = 7 × 13

112 = 2 × 2 × 2 × 2 × 7

49 = 7 × 7

∴ HCF of 91, 112 and 49 is 7.

(i) 18, 54, 81

Solution: The HCF of 18, 54 and 81 can also be found by prime factorization of these numbers as follows:

Thus, 18 = 2 × 3 × 3

54 = 2 × 3 × 3 × 3

81 = 3 × 3 × 3 × 3

∴ HCF of 18, 54 and 81 is 3 × 3 = 9.

(j) 12, 45, 75

Solution: The HCF of 18, 54 and 81 can also be found by prime factorization of these numbers as follows:

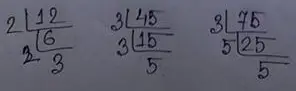
Thus, 12 = 2 × 2 × 3

45 = 3 × 3 × 5

75 = 3 × 5 × 5

∴ HCF of 12, 45 and 75 is 3.

(2) What is the HCF of two consecutive?     

Ans: (a) Numbers = 1

(b) Even numbers = 2

(c) Odd numbers = 1

(3) HCF of co-prime numbers 4 and 15 was found as follows by factorization: 4 = 2 × 2 and 15 = 3 × 5 since there is no common prime factor, so HCF of 4 and 15 is 0. Is the answer correct? If not, what is the correct HCF?

Ans: No; the correct HCF is 1.